By Abhishek Panigrahi, Bingbin Liu, Sadhika Malladi, Sham Kakade and Surbhi Goel
This post is based on “In Good GRACEs: Principled Teacher Selection for Knowledge Distillation” by Abhishek Panigrahi, Bingbin Liu, Sadhika Malladi, Sham Kakade, and Surbhi Goel
TL; DR Training students on teacher-generated responses can significantly improve math reasoning in small models, but selecting the right teacher remains an open question. We introduce GRACE, a cost-efficient gradient-based score that ranks teachers without training the student. On MATH and GSM8K, GRACE achieves up to 86% correlation with the final student performance. When used for teacher selection, the selected teacher enables students to reach within 0.3% of the best achievable performance, outperforming intuitive baselines such as teacher accuracy and student perplexity.

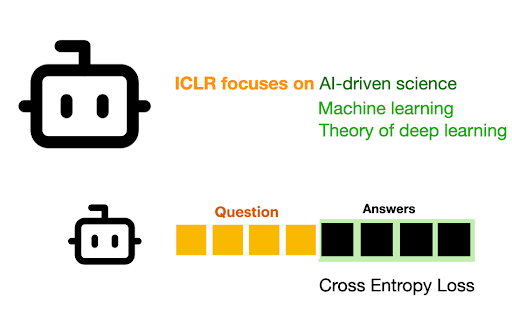
Knowledge distillation with teacher generations
Knowledge distillation has been a cornerstone technique for improving small models Hinton et al. 2015, with a simple idea of training a smaller model (student) to mimic the output of a larger, more capable model (teacher). In the current era of language models, a popular variant of knowledge distillation is to generate multiple responses of a good teacher on a given set of questions and train a small model on the responses of the teacher with cross entropy loss (e.g. OpenThoughts, Guha et al. 2025).
While distillation can result in powerful small language models that solve surprisingly hard problems, it can also be brittle: changing the teacher’s model family, size, or even generation temperature can change student performance. Given the numerous possible design choices for knowledge distillation, we ask whether it is possible to define a teacher score that selects the best teacher without training a student for every candidate.

(Left) Teachers from different model families.
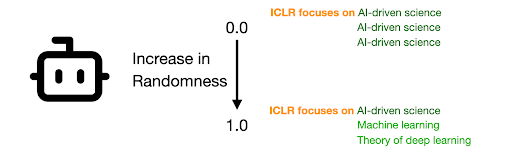
(Right) Generation temperature controls response diversity.
Designing such a score is not as straightforward as it might seem. A counterintuitive observation is that higher-performing teachers do not always lead to better students. Prior work has attributed this phenomenon to a “capacity gap” between teacher and student (Mirzadeh et al. 2019), where students struggle to learn when the gap is too large, and recent language model experiments report similar findings (Busbridge et al., 2024, Kang et al., 2025). Moreover, other common heuristics such as response length, or the student’s initial loss on teacher-generated data all fail to serve as a reliable score.
In this work, we introduce GRACE, a lightweight gradient-based score that selects teachers with consistently low regret across model families, sizes, and scales—without training students. As a bonus, we show that GRACE can also guide key distillation choices, such as selecting the optimal teacher generation temperature.
Selecting the right teacher with GRACE
GRACE studies the distribution of gradients of the student on the teacher generated data at the start of training. Its design centers around two key properties: teacher’s generation diversity, and teacher-student alignment.
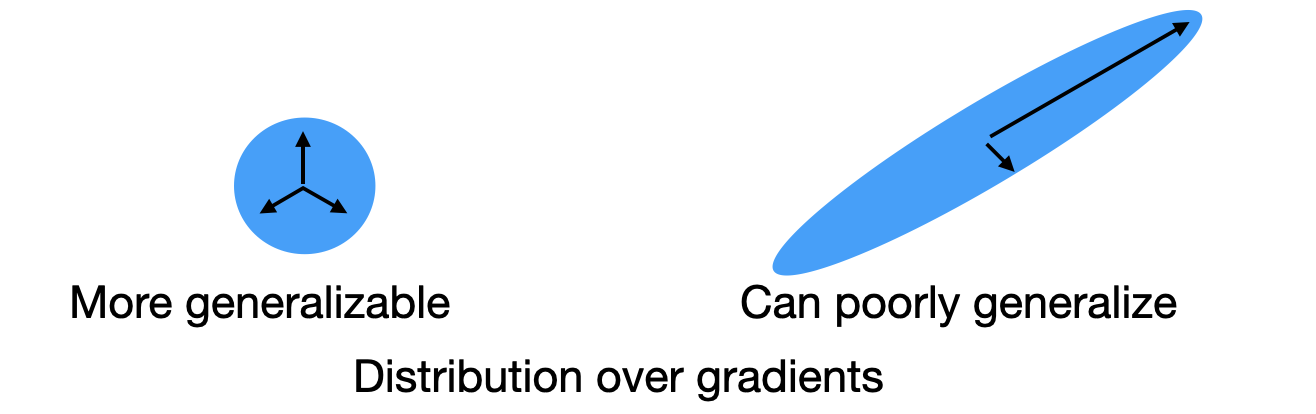
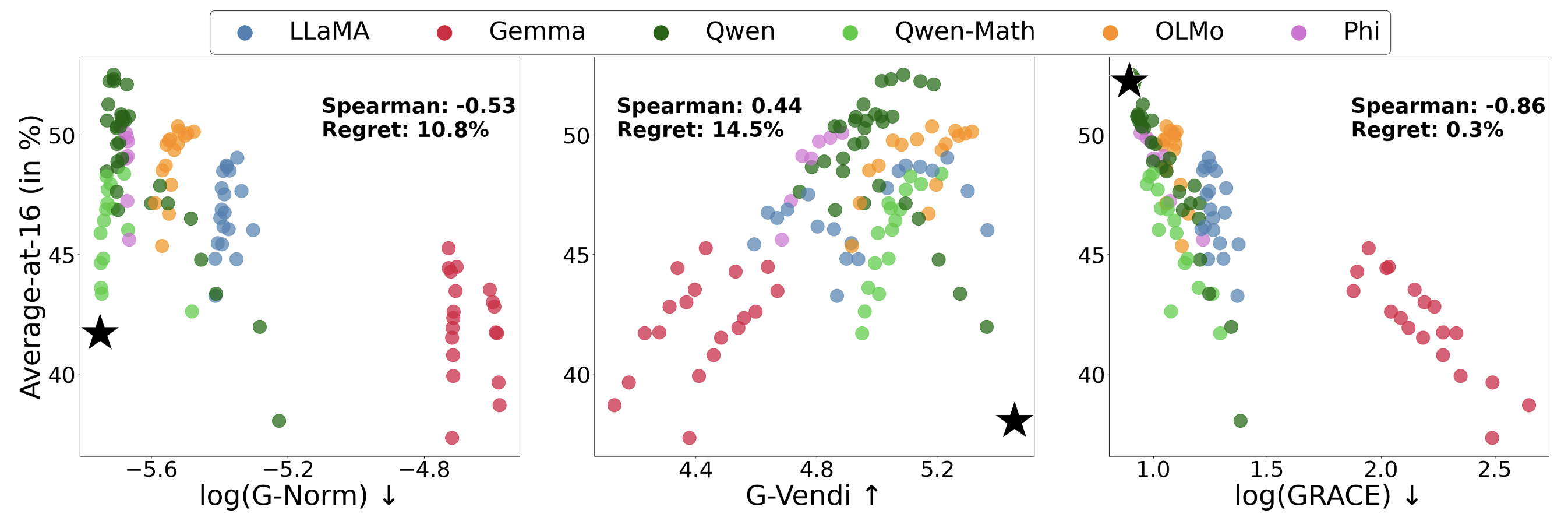
Diversity, measured by the gradient spectrum (G-Vendi). Motivated by Jung et al. (2025), we observe that teachers producing diverse responses per question are more effective for distillation. We measure this diversity using the spectrum of normalized student gradients. A high-entropy spectrum indicates varied and non-redundant learning signals, effectively acting like a larger and more informative training set.
Teacher-student alignment, measured by the gradient norm (G-Norm). A good teacher is one whose data requires only small updates to the student. The gradient norm provides a coarse measure of how much the student must change to fit the teacher’s outputs. Smaller norms indicate better alignment with the student’s current representation.
Looking at just one signal fails: We find that neither signal alone is sufficient. G-Vendi can overvalue random diversity. For example, when the student is used as its own teacher, it achieves the highest G-Vendi score, yet self-distillation yields only 4 percent accuracy. Conversely, G-Norm ignores the directional diversity of gradients and is therefore also inadequate.
Thus, effective teachers must be both diverse and aligned.
Designing GRACE:
Rather than measuring magnitude and diversity separately, GRACE asks a more precise question:
Are the gradients induced by this teacher uniformly small across meaningful directions?
To operationalize this idea, we measure the magnitude of gradients weighted under the inverse spectrum of normalized gradients. A key ingredient is a cross-validation structure.
Concretely, we take a small subset of data and randomly split it into two parts. From one split, we learn the main directions in which the teacher pushes the student by looking at the spectrum of normalized gradients. From the other split, we measure how large the gradients are along those directions.
Intuitively, large gradients along directions with small eigenvalues are especially problematic, as they can lead to unstable updates and high variance during training. GRACE therefore penalizes such cases more strongly. As a result, GRACE prefers teachers that provide gradient signals that are both well-distributed and small across all directions.
More formally, let $D$ be a subset of the data, randomly split into two parts $D_1$ and $D_2$. Let $g$ denote the gradient induced by a single example. We define
\[\mathbb{E}_{g \sim D_1} \left[ g^\top \tilde{\Sigma}_2^{-1} g \right] \;=\; \mathbb{E}_{g \sim D_1} \sum_i \frac{1}{\sigma_i} \, (g^\top v_i)^2,\]where
\[\tilde{\Sigma}_2 \;=\; \mathbb{E}_{g \sim D_2} \left[ \frac{g}{\lVert g \rVert_2} \frac{g^\top}{\lVert g \rVert_2} \right],\]and ${(\sigma_i, v_i)}$ denote the eigenvalue–eigenvector pairs of $\tilde{\Sigma}_2$.

GRACE relates to a measure of generalization
GRACE is closely connected to leave-one-out conditional mutual information (CMI), a standard tool in generalization theory (Xu & Raginsky, 2017; Steinke & Zakynthinou, 2020; Rammal et al., 2022).
From this perspective, GRACE measures the sensitivity of a gradient update to a subset of the training data. If removing a few teacher responses significantly alters the update, learning from the teacher is brittle and unlikely to generalize. If the update remains stable, the teacher provides robust learning signals. CMI formalizes this notion of stability.
Experimental results
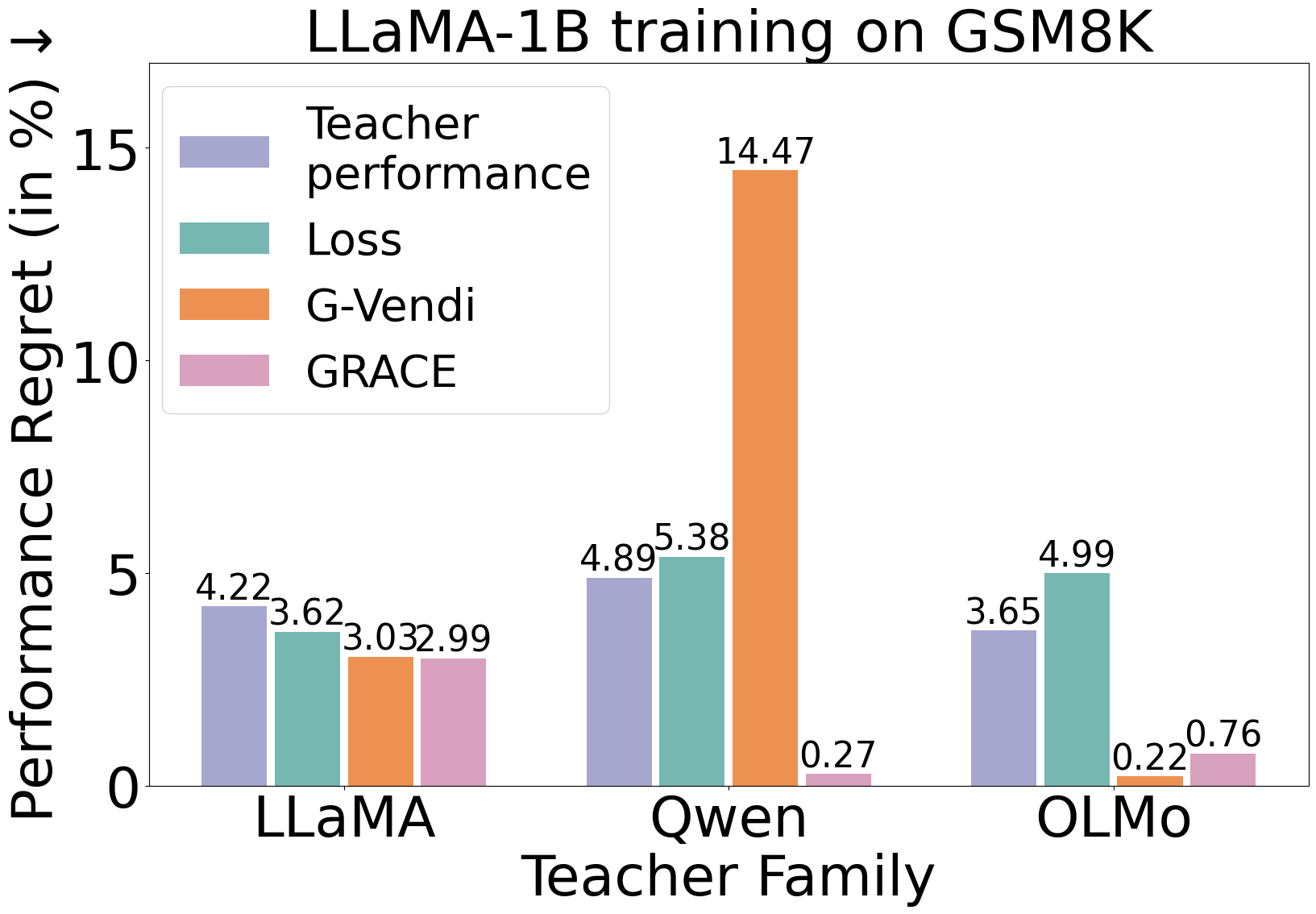
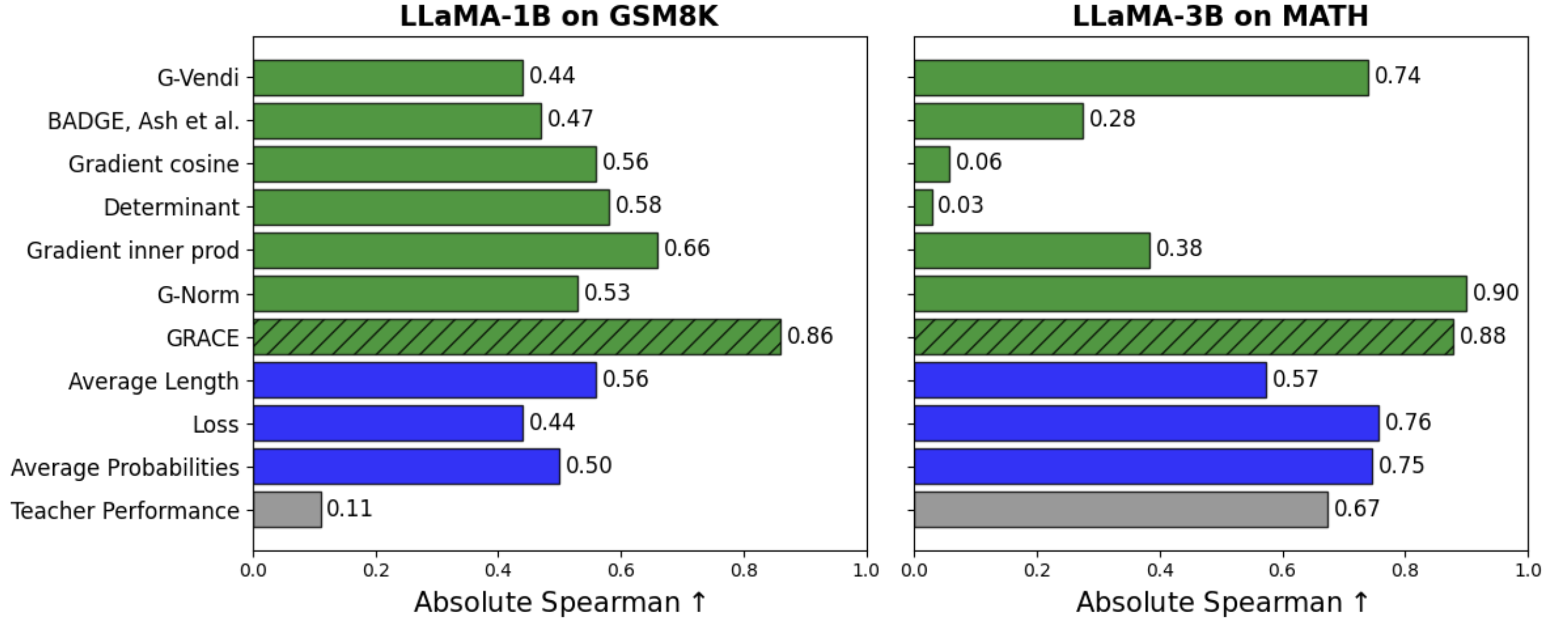
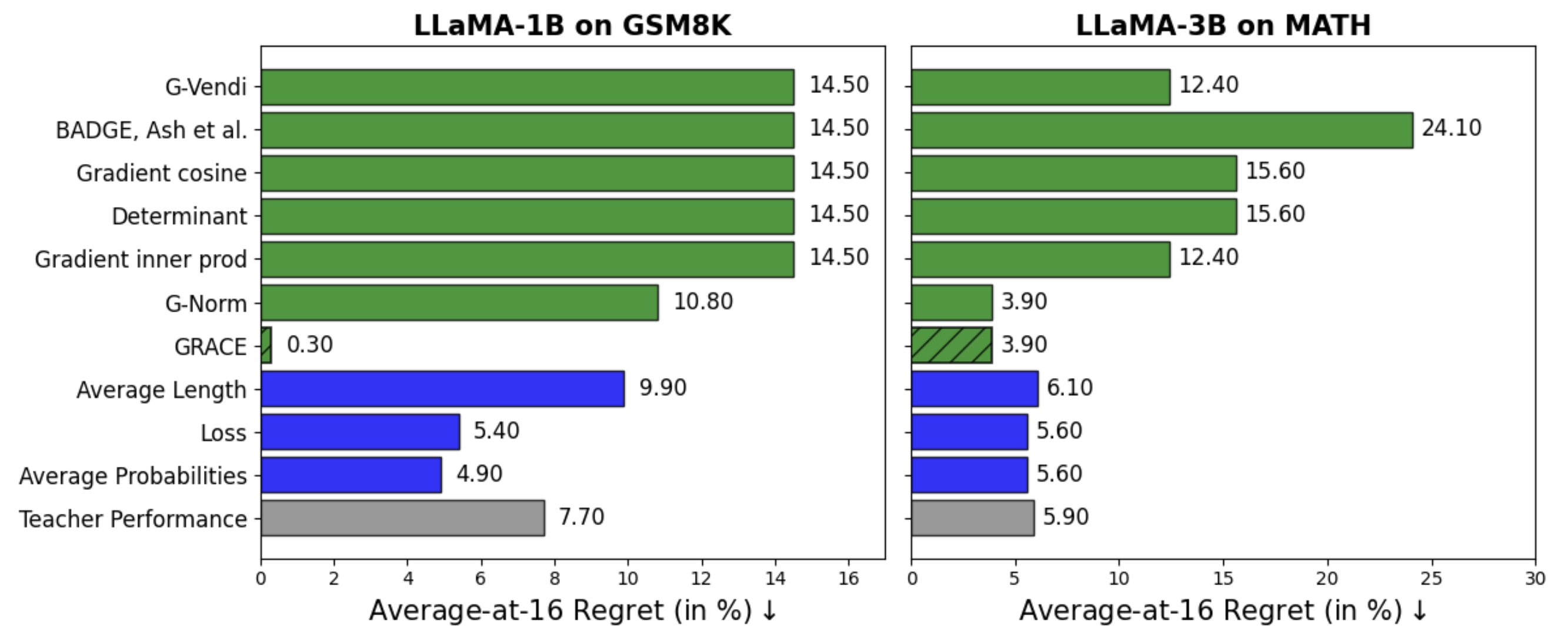
We evaluate GRACE across multiple student models: LLaMA-1B, OLMo-1B, and Gemma-2B on GSM8K, and LLaMA-3B on MATH. Our teacher pool consists of 120 teacher generation setups: we consider a combination of 15 models spanning five model families (Gemma, LLaMA, OLMo, Phi, and Qwen or Qwen-Math), and 8 generation temperatures per teacher in the range of [0.3, 1.0].
To assess the effectiveness of a score at teacher selection, we compare along two axes: (1) correlation with final student performance, and (2) regret, defined as the performance gap between the student trained using the selected teacher and the best achievable student. Student performance is measured using Average@16, the accuracy averaged over 16 generations per question.
GRACE identifies good teachers
GRACE achieves the highest correlation with final student performance and the lowest regret among all teacher selection scores across all students and math tasks. For example, when training LLaMA-1B on GSM8K, GRACE achieves an 86% correlation with student performance across all teachers and incurs only 0.3% regret when used to select the best teacher.
Importantly, both components of GRACE, the gradient norm and the gradient spectrum, are required for optimal performance. Either component on its own, as measured by G-norm or G-Vendi, is insufficient.
GRACE guides distillation design choices
We can break down the behavior of GRACE along 3 axes of teacher choice: temperature of generation from the teacher, the size of the teacher and the teacher family.
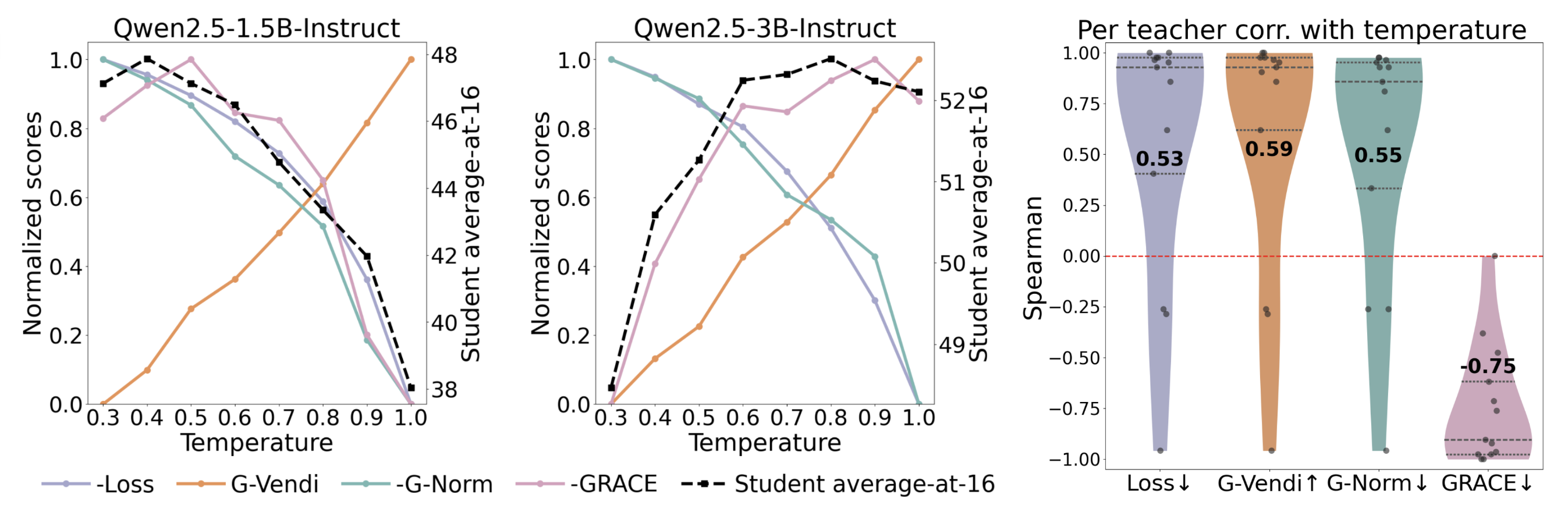
Identifying the optimal generation temperature. Generation temperature has a surprisingly large impact on distillation performance, yet in practice it is often chosen by trial and error. GRACE offers a principled alternative.
As a case study, we analyze Qwen teachers distilled into a LLaMA-1B student. We find that the optimal temperature depends strongly on the teacher: for the 3B teacher it is 0.8, while for the 1.5B teacher it is 0.4. GRACE remarkably predicts optimal temperatures of 0.9 and 0.5 respectively. When aggregated across all teachers, GRACE achieves a remarkable 75% correlation with final student performance.
Teacher selection under size or family constraints. Beyond temperature, we study teacher selection under size budgets and within model families. Across both axes, GRACE consistently achieves high correlation with student performance and near zero regret, substantially outperforming G-Norm and G-Vendi.
Limitations & Future research
While GRACE performs well in practice, an important future direction is to make it robust to adversarial settings, such as when a teacher produces repetitive or degenerate outputs that artificially reduce gradient magnitudes. Although we did not observe such cases in practice, fully characterizing additional failure modes of GRACE remains an open question.
Beyond gradient diversity and alignment, GRACE could benefit from incorporating additional signals about the teacher and the data. While it deliberately avoids using teacher logits, using logit information where available may further improve performance of GRACE. GRACE also opens the door to adaptive distillation, where teacher choice can change across training stages or data subsets.